Ohessa materiaali, jota käsittelimme kurssilla ja joka naputeltiin koneelle.
R-komennot:
http://users.utu.fi/attenka/R_pikakurssi061214.R
Midi-fileen csv-muotoinen lista, jota käytettiin 4:ssä sovelluksessa melodioiden generoimiseksi:
http://users.utu.fi/attenka/tangerine8.csv
IH:n generoima melodia:
http://users.utu.fi/attenka/ilenmelodi.mid
R:stä löytyy matriisioperaatioihin myös tehokkaat apply, sapply, tapply, mapply-komennot, mutta niitä ei nyt otettu, vaan tulimme for-luupilla toimeen. Ehkäpä katsomme niitä jossain vaiheessa.
Saturday, December 16, 2006
Thursday, December 14, 2006
R-pikakurssista
Laitan myöhemmin oman pikakurssimme materiaalin tänne saataville, mutta ohessa linkki erinomaiseen R-ohjelmointia käsittelevään dokumenttiin, jonka on kirjoittanut Pasi Koikkalainen.
http://erin.mit.jyu.fi/pako/CourseR/Osa1234.pdf
http://erin.mit.jyu.fi/pako/CourseR/Osa1234.pdf
Monday, December 04, 2006
Ilmainen MidiSwing-sekvensseri
Tein pyynnöstä suomenkieliset käännökset MidiSwing-nimisen ilmaisen midisekvensseriohjelman komentoihin. Käännökset vaativat vielä hiomista ja jos löytyy joku suomenkielinen, jolle midi-termistö on tuttu, hän voisi esittää parannusehdotuksia käännöksiin ohjelman kehittäjälle Pascal Naidonille. Osa käännöksistä vielä puuttuu.
Sekvensserin voi asentaa OS X:ään, Windowsiin ja Linuxiin (!). Nyt kun ohjelmasta näkee suoraan, miten käännökset sijoittuvat ohjelman eri osiin ikkunassa ja komentovalikossa (ne tehdään erilliselle listalle englanninkielisten termien rinnalle), kääntäminen on helpompaa kuin sokkona listaan tehtäessä. Ohjelman kotisivut löytyvät täältä:
http://www.les-stooges.org/pascal/midiswing/index.php?la=en#top
Sekvensserin voi asentaa OS X:ään, Windowsiin ja Linuxiin (!). Nyt kun ohjelmasta näkee suoraan, miten käännökset sijoittuvat ohjelman eri osiin ikkunassa ja komentovalikossa (ne tehdään erilliselle listalle englanninkielisten termien rinnalle), kääntäminen on helpompaa kuin sokkona listaan tehtäessä. Ohjelman kotisivut löytyvät täältä:
http://www.les-stooges.org/pascal/midiswing/index.php?la=en#top
Thursday, November 23, 2006
R-pikakurssin ajankohta siirtyy
Päätimme I.H.:n kanssa siirtää R-pikakurssin ajankohtaa myöhemmäksi, jotta saamme ainakin JR:n mukaan. Pidämme kurssin 13.-14.12.2006.
Saturday, November 18, 2006
Merkittävä nuotinnusohjelma Sibelius-Akatemiasta
Olin seuraamassa Mika Kuuskankareen väitöstilaisuutta tänään lauantaina 18.11. Kuuskankareen väitöksen aiheena oli hänen kehittämänsä ENP-nuotinnusjärjestelmä, joka on osa PWGL-nimistä, erityisesti säveltäjille ja musiikinteoreetikoille suunnattua ohjelmistoa. Väitöstilaisuus oli demoineen vaikuttava. Vastaväittäjänä toimi Roger B. Dannenberg Carnegie Mellon yliopistosta. PWGL:n beta-versio Mac OSX:lle ja Windowsille on ladattavissa osoitteesta http://www2.siba.fi/PWGL/downloads.html
Lisätietoa ohjelmasta löytyy sivulta http://www.siba.fi/fin/ajankohtaista/kuuskankare/
Lisätietoa ohjelmasta löytyy sivulta http://www.siba.fi/fin/ajankohtaista/kuuskankare/
Wednesday, November 15, 2006
R-pikakurssi 24. ja 27.11.
Pidän R:n pikakurssin pe 24.11. klo 9-15 ja ma 27.11. klo 9-12. Perjantaina aloitamme musiikkitieteen tiloissa Salongissa, mutta klo 12 eteenpäin voimme halutessamme jatkaa Educariumin luokassa 155 eli samaisessa luokassa, jossa TKAMT:n kurssi pidettiin viime keväänä. Tämä tila on varattu meille myös maanantaina.
Tiedoksi merkittävä tietokoneavusteiseen musiikintutkimukseen ja musiikin generointiin liittyvä tapahtuma eli Mika Kuuskankareen ENP-nuotinkirjoitusohjelmaa käsittelevä väitöstilaisuus pidetään Sibelius-Akatemiassa 18.11. klo 12.
Tiedoksi merkittävä tietokoneavusteiseen musiikintutkimukseen ja musiikin generointiin liittyvä tapahtuma eli Mika Kuuskankareen ENP-nuotinkirjoitusohjelmaa käsittelevä väitöstilaisuus pidetään Sibelius-Akatemiassa 18.11. klo 12.
Saturday, October 14, 2006
Oppimispäiväkirjani palautetuista oppimispäiväkirjoista
Kirjoitin alla mainitusta luennosta "oppimispäiväkirjan" saamieni oppimispäiväkirjojen perusteella. Se löytyy tästä.
Monday, October 02, 2006
WAP 9.10. 2006 pidettävää luentoani varten
Ohessa vielä yksi, hiukan "Afrikan tähden" pelilautaa muistuttava malli WAP:ista ;-) Olen sitä varten koonnut joukon mahdollisia tkamt:een liittyviä termejä luentoa Tietokoneavusteinen musiikintutkimus 9.10 varten ja annoin tällä kertaa korrelaatiotaulukkoon vain joko arvon 0 tai 1 sen mukaan, liittyvätkö asiat luennolla toisiinsa vahvasti vai eivät. Punaisella solmulla ja isommalla tekstillä merkityt - sumean näköisesti valitut - termit viittaavat luennon "pilareihin". Tulos on tämän näköinen:

Sunday, September 24, 2006
Painotettu assosiaatiokartta
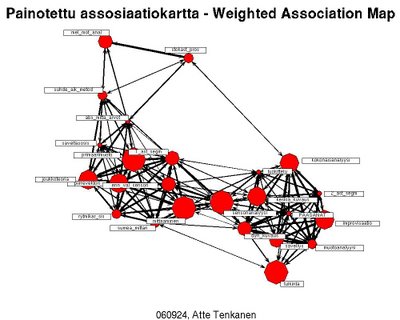
Kuva tulee näkyviin suurempana klikkaamalla sitä.
R:llä voi tehdä monenlaista musiikintutkimukseen liittyvää, myös hiukan sumeampia juttuja kuin mitä tässä on aikaisemmin ollut esillä.
Ohessa on malli kuvauksesta, jonka olen nimennyt "painotetuksi assosiaatiokartaksi". Se on hiukan kuin mind map, mutta sitä varten täytyy parametrit tuntea ennestään, eikä niiden järjestelemiseksi tarvitse itse nähdä vaivaa, sijoittelun tekee kone. PAK:aa varten olen symmetriseen n x n -taulukkoon merkinnyt riveihin ja sarakkeisiin tutkimukseeni liittyviä pääsanoja ja kirjannut soluihin intuitiivisesti niiden väliset "assosiaatioarvot" (välillä [0-1], 0=ei assosiaatiota, 1=maksimi yhteys). Sen jälkeen olen piirrättänyt oheisen kartan R:llä.
Miksi tällainen kartta, mitä hyötyä siitä on?
Jos päässäsi on paljon asiaa, muttet pysty laittamaan pääasioitasi järjestykseen, voit verrata jokaista valitsemaasi käsitettä muihin käsitteisiin kirjaamalla niiden assosiaatioarvot taulukkoon (siis arvioiden esim. välillä 0-1) hyvin mekaanisella tavalla koettamatta sen enempää hahmottaa, mikä on aihealueen kokonaiskuva. Sen jälkeen moniulotteisella skaalauksella tai vastaavilla menetelmillä voi luoda itselleen oheisen tyyppisen kartan. R:ään löytyy valmiina sna-niminen kirjasto, joka sisältää gplot-komennon, jolla oheinen kuva on tehty. gplot() piirtää myös assosiaatioita kuvaavat nuolet, toisin kuin esim. peruspakettiin sisältyvä moniulotteisen skaalauksen luova mds-komento.
Ideaa käsittelevä sivu löytyy täältä.
Algoritmi PAK:n tekemiseksi R:llä:
# Käsitteiden nimet vektoriin.
TERMIT=c("mittaaminen","luokittelu","stokast_pros","tulkinta","joukkoteoria","primaarimuoto", "sumea_mittari", "dyn_kuvaus","keskiarvo_kuvaus")
# matriisin alustaminen, nollat NA:iden paikalle (ei välttämätön):
KASITEMATRIISI<-diag(length(TERMIT)) # luodaanpa saman tien ns. identiteettimatriisi
# nimet riveille ja sarakkeisiin
row.names(KASITEMATRIISI)<-TERMIT
KASITEMATRIISI=t(KASITEMATRIISI)
row.names(KASITEMATRIISI)<-TERMIT
fix(KASITEMATRIISI)# Tämä komento avaa taulukon, jonka avulla on helppo sijoittaa arvot paikalleen, kirjoita arvot vain soluihin ykkösten alle, seuraava luuppi luo symmetrisen matriisin. Aloita kaksoisklikkaamalla soluun rivillä 2, sarakkeeseen 1 ja kirjoita esim. ".5". Sen jälkeen paina enter ja kirjoita seur. soluun arvo.
for(i in 1:length(KASITEMATRIISI[,1]))
{ # huom. kaarisulut "{"
for(j in 1:length(KASITEMATRIISI[,1]))
{
KASITEMATRIISI[i,j]=KASITEMATRIISI[j,i]
}
}
# ladataan sna-kirjasto, hae se kuitenkin ensin: install.packages("sna")
library(sna)
# Tehdään kuva:
set.seed(123)
kor <- cor(KASITEMATRIISI)
X11() # avaa ikkunan kuvaa varten, Winissa voi käyttää window(), Macissa quartz()
gplot(sign(kor), edge.lwd = 10*kor, displaylabels = TRUE, label = rownames(kor), vertex.cex=as.vector(colSums(KASITEMATRIISI))/2)
# kokeile myös parametrilla mode="mds" eli:
#gplot(sign(kor), edge.lwd = 10*kor, displaylabels = TRUE, label = rownames(kor), mode="mds")
title("Painotettu assosiaatiokartta - Weighted Association Map", cex.main=2)
Saturday, July 22, 2006
Rekursio R:llä
R:llä voi tehdä myös rekursiivisen kutsun, jossa siis funktion sisällä kutsutaan funktiota itseään:
# Funktio kertoma rekursiona R:llä:
kertoma <- function(luku){
if (luku > 1){
return(kertoma(luku-1)*luku)}
else return(1)
}
# Esimerkki funktion käytöstä:
#> kertoma(7)
#[1] 5040
# Funktio kertoma rekursiona R:llä:
kertoma <- function(luku){
if (luku > 1){
return(kertoma(luku-1)*luku)}
else return(1)
}
# Esimerkki funktion käytöstä:
#> kertoma(7)
#[1] 5040
R-wiki netissä
R:ää käsittelevä wiki löytyy osoitteesta
http://wiki.r-project.org/rwiki/doku.php
Olen alustavasti katsellut jonkinlaisen R-pikakurssin sisältöä kevään kurssin pohjalta ja toivon saavani sen valmiiksi elokuun aikana.
http://wiki.r-project.org/rwiki/doku.php
Olen alustavasti katsellut jonkinlaisen R-pikakurssin sisältöä kevään kurssin pohjalta ja toivon saavani sen valmiiksi elokuun aikana.
Sunday, May 28, 2006
Tilastotiedettä soveltajille
Tommi Viitasen opuksen "Tilastotiedettä soveltajille" pdf-versio löytyy osoitteesta
http://users.utu.fi/totavi/
Kirjassa neuvotaan, kuinka tilastolaskennan perusmenetelmät hoituvat R:llä. Jostain syystä sivua ei löydy enää Googlettamalla. Laitoin sen siksi tänne.
http://users.utu.fi/totavi/
Kirjassa neuvotaan, kuinka tilastolaskennan perusmenetelmät hoituvat R:llä. Jostain syystä sivua ei löydy enää Googlettamalla. Laitoin sen siksi tänne.
Thursday, May 25, 2006
Kurssin loppuraportti 24.5.2006
Tein yliopistopedagogiikan kurssia varten loppuraportin tästä hankkeesta ja ohessa on sen tiivistelmä.
Turun yliopisto
Yliopistopedagogiikan
hankeraportin tiivistelmä
Atte Tenkanen
24.5.2006
Asetin kurssille moniakin tavoitteita, mutta toisaalta lähdin liikkeelle sillä periaatteella, että katsotaan, mitä ehditään. Tärkein tavoitteistani oli esitellä erilaisia mahdollisuuksia kvantitatiivisten musiikkiaineistojen analyysiin. Tämä tavoite lienee täyttynytkin, muut tavoitteista jäivät enemmän tai vähemmän saavuttamatta. Asetin itselleni opettajana tavoitteeksi sen, että oppiminen ja opitut asiat koetaan mielekkäiksi ja mielenkiintoisiksi.
Sain hyviä neuvoja ja ideoita yliopistopedagogiikkakurssilta ja järjestelin aihealueeseen liittyviä asioita mm. mind mapin avulla. Valmista kurssimateriaalia en löytänyt, vaan valmistin sen käytännössä itse. Halusin rakentaa kurssin alusta lähtien mahdollisimman hyvin, mutta huomasin pian, ettei aika riitä lainkaan kaikkeen siihen, mitä olin suunnitellut ja mitä tuli oppituntien valmistamiseen. Tein luentoja varten powerpoint-esityksiä ja algoritmejä, jotka kaikki löytyvät kurssiani varten perustamaltani weblog-sivulta.
(ks. http://musiikintutkimus.blogspot.com , ts. tämä sivu ;-).
Tein 1. periodin lopuksi välitentin, jonka tarkoituksena oli kartoittaa sitä, miten asiat oli ymmärretty. Perustin lopuksi antamani arvosanat pitkälti tämän tentin arvosanoihin. Toisella periodilla kahden opiskelijan esittelemät omat sovellukset toivat lisää mielenkiintoa ja sisältöä kurssiin. Koin nämä luennot itse erityisen antoisiksi.
Ohessa muutamia poimintoja saamastani palautteesta kysymykseen, vastasiko kurssi odotuksiasi?
“Osittain. Aiheen esittelemisen osalta kurssi toimi mallikkaasti. Tunneilla näytettiin laaja kirjo erilaisia sovellusmahdollisuuksia. Nämä näytteet olivat mielestäni onnistuneesti valittu.”
“Odotin kurssilta ehkä ripauksen enemmän myös käytännönläheisyyttä.”
Pelkäsin hiukan sitä, että kurssista tulee liian raskas kotitehtävineen, jos se on sitä jo teoreettisten käsitteidensä puolesta. Asioiden opiskeluun liitettävät "ajattelua aktivoivat" tehtävät jäivät puuttumaan ja niin muodoin myös palautteen antaminen opiskelijoille. Kurssini luennoille poikkesi kaksi yliopistopedagogiikkaan osallistunutta henkilöä ja heiltä saamani palaute oli - oikeastaan yllättäen - rohkaisevaa. Tämä antaa itselleni itsevarmuutta mahdollisesti tuleviin tehtäviin.
Opin kurssin aikana paljon. Siitä oli minulle itselleni hyötyä niin opettajana kuin myös aiheeseen liittyvien uusien ideoiden ja syntyneiden sovellusten vuoksi. Yliopiston viikkoluentoihin perustuva opetus on monessa tapauksessa ehkä ainoa mahdollinen opetusmalli, mutta pienemmissä oppiaineissa ja esimerkiksi oman kurssini tyyppisissä tilanteissa intensiivinen, esimerkiksi viikon pituinen periodi, jossa työskenneltäisiin vaikkapa 6 tuntia päivässä, toimisi varmasti paremmin kuin pitkin periodeja levitetyt tunnit.
Kurssia varten valmistamastani materiaalista on nyt helpompi lähteä eteenpäin, mikäli vastaavantyyppiselle kurssille on joskus tarvetta. Tarkoitukseni on joka tapauksessa järjestää kurssin aikana valmistamani ohjelmointiin liittyvä materiaali käyttökelpoiseksi oheismateriaaliksi esimerkiksi itseopiskelua varten kommentteineen. Saattaapa ohjelmointiin keskittyvä intensiivikurssikin vielä toteutua.
Turun yliopisto
Yliopistopedagogiikan
hankeraportin tiivistelmä
Atte Tenkanen
24.5.2006
Tietokoneavusteinen musiikintutkimus (S1f, 7 op)
Pioneerikurssi - niin itselleni kuin oppiaineelleni
Kurssi Tietokoneavusteinen musiikintutkimus (S1f, 7 op) kuului osana Turun yliopiston, Åbo Akademin ja Turun ammattikorkeakoulun Musicare- yhteishanketta. Kurssille ilmoittautui alun alkaen 9 ihmistä ja sen kävi loppuun 6. Luennot pidettiin perjantaiaamuisin klo 8.30-10.00. Vastaavaa kurssia ei ole Turun yliopiston musiikkitieteen oppiaineessa aikaisemmin järjestetty, joten kyseessä oli pioneerityö. Sitä se oli myös itselleni, joten odotin alusta asti haasteita.Pioneerikurssi - niin itselleni kuin oppiaineelleni
Asetin kurssille moniakin tavoitteita, mutta toisaalta lähdin liikkeelle sillä periaatteella, että katsotaan, mitä ehditään. Tärkein tavoitteistani oli esitellä erilaisia mahdollisuuksia kvantitatiivisten musiikkiaineistojen analyysiin. Tämä tavoite lienee täyttynytkin, muut tavoitteista jäivät enemmän tai vähemmän saavuttamatta. Asetin itselleni opettajana tavoitteeksi sen, että oppiminen ja opitut asiat koetaan mielekkäiksi ja mielenkiintoisiksi.
Sain hyviä neuvoja ja ideoita yliopistopedagogiikkakurssilta ja järjestelin aihealueeseen liittyviä asioita mm. mind mapin avulla. Valmista kurssimateriaalia en löytänyt, vaan valmistin sen käytännössä itse. Halusin rakentaa kurssin alusta lähtien mahdollisimman hyvin, mutta huomasin pian, ettei aika riitä lainkaan kaikkeen siihen, mitä olin suunnitellut ja mitä tuli oppituntien valmistamiseen. Tein luentoja varten powerpoint-esityksiä ja algoritmejä, jotka kaikki löytyvät kurssiani varten perustamaltani weblog-sivulta.
(ks. http://musiikintutkimus.blogspot.com , ts. tämä sivu ;-).
Tein 1. periodin lopuksi välitentin, jonka tarkoituksena oli kartoittaa sitä, miten asiat oli ymmärretty. Perustin lopuksi antamani arvosanat pitkälti tämän tentin arvosanoihin. Toisella periodilla kahden opiskelijan esittelemät omat sovellukset toivat lisää mielenkiintoa ja sisältöä kurssiin. Koin nämä luennot itse erityisen antoisiksi.
Ohessa muutamia poimintoja saamastani palautteesta kysymykseen, vastasiko kurssi odotuksiasi?
“Osittain. Aiheen esittelemisen osalta kurssi toimi mallikkaasti. Tunneilla näytettiin laaja kirjo erilaisia sovellusmahdollisuuksia. Nämä näytteet olivat mielestäni onnistuneesti valittu.”
“Odotin kurssilta ehkä ripauksen enemmän myös käytännönläheisyyttä.”
Pelkäsin hiukan sitä, että kurssista tulee liian raskas kotitehtävineen, jos se on sitä jo teoreettisten käsitteidensä puolesta. Asioiden opiskeluun liitettävät "ajattelua aktivoivat" tehtävät jäivät puuttumaan ja niin muodoin myös palautteen antaminen opiskelijoille. Kurssini luennoille poikkesi kaksi yliopistopedagogiikkaan osallistunutta henkilöä ja heiltä saamani palaute oli - oikeastaan yllättäen - rohkaisevaa. Tämä antaa itselleni itsevarmuutta mahdollisesti tuleviin tehtäviin.
Opin kurssin aikana paljon. Siitä oli minulle itselleni hyötyä niin opettajana kuin myös aiheeseen liittyvien uusien ideoiden ja syntyneiden sovellusten vuoksi. Yliopiston viikkoluentoihin perustuva opetus on monessa tapauksessa ehkä ainoa mahdollinen opetusmalli, mutta pienemmissä oppiaineissa ja esimerkiksi oman kurssini tyyppisissä tilanteissa intensiivinen, esimerkiksi viikon pituinen periodi, jossa työskenneltäisiin vaikkapa 6 tuntia päivässä, toimisi varmasti paremmin kuin pitkin periodeja levitetyt tunnit.
Kurssia varten valmistamastani materiaalista on nyt helpompi lähteä eteenpäin, mikäli vastaavantyyppiselle kurssille on joskus tarvetta. Tarkoitukseni on joka tapauksessa järjestää kurssin aikana valmistamani ohjelmointiin liittyvä materiaali käyttökelpoiseksi oheismateriaaliksi esimerkiksi itseopiskelua varten kommentteineen. Saattaapa ohjelmointiin keskittyvä intensiivikurssikin vielä toteutua.
Tuesday, May 02, 2006
Kevään viimeinen luento 16.5. klo 15
Sovimme, että viimeinen tapaaminen on ti 16.5. klo 15.
Tiistaina ajattelin tarkastella yläsävelsarjaa. Asiahan on ollut ajankohtainen aina Pythagoraasta lähtien ja jaksaa yhä kiinnostaa. Sovelluksia voisi kuvitella löytyvän myös vaikka kuinka paljon. Liittyyhän yläsävelsarja tavalla tai toisella esimerkiksi sellaisiin käsitteisiin kuin äänen väri, intonaatio, (spektraali-)harmonia, asteikot, viritysjärjestelmät, tonaalisuus, konsonoivuus, dissonoivuus ym. ym. Esim. kritisoidulle Krumhansl-Kessler-algoritmille voisin kuvitella kehitettävän yläsävelsarjaa hyödyntävän vastineen, rinnakkaisen algoritmin, joka perustuisi puhtaasti matemaattisiin suhteisiin toisin kuin K-K-systeemi. Se, olisiko sillä jotain yhteyttä havaintoon tai tonaalisesti suuntautuneeseen korvaan, on eri juttu. Myös Huronin konsonanssifunktion tapainen yläsävelsarjaan perustuva konsonoivuutta mittaava systeemi lienee mahdollinen (?)
Jos haluat laskea tasavireisen järjestelmän taajuudet (a1=440 Hz), ne saa oheisella funktiolla.
pitchfreq=function(n){27.5*2^((n-21)/12)}
Funktiolle annetaan syötteenä midisävelkorkeus. 27.5 Hz on alimman pianosta löytyvän sävelen taajuus. Taajuus kasvaa eksponentiaalisesti suhteessa puolisävelaskeliin tuollaisella kaavalla. Kokeile:
pitchfreq(60); # c1
pitchfreq(69); # a1
Jos haluat tulostaa kaikki pianosta löytyvät perustaajuudet, kokeile:
for(n in 21:108){print(pitchfreq(n))}
Oheinen kuva on luotu skriptillä, joka koettaa sovittaa yläsävelsarjaa annettuun sävelkorkeuksien joukkoon ja tulostaa tämän harmonian todennäköisen pohjasävelen. Funktiossa on vielä parantamisen varaa... Parsifal-alkusoitosta on laskettu tahtikohtaisesti pohjasävelet. Klikkaa kuvaa nähdäksesi sen suurempana.
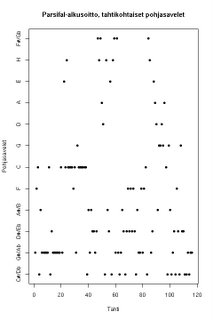
Tiistaina ajattelin tarkastella yläsävelsarjaa. Asiahan on ollut ajankohtainen aina Pythagoraasta lähtien ja jaksaa yhä kiinnostaa. Sovelluksia voisi kuvitella löytyvän myös vaikka kuinka paljon. Liittyyhän yläsävelsarja tavalla tai toisella esimerkiksi sellaisiin käsitteisiin kuin äänen väri, intonaatio, (spektraali-)harmonia, asteikot, viritysjärjestelmät, tonaalisuus, konsonoivuus, dissonoivuus ym. ym. Esim. kritisoidulle Krumhansl-Kessler-algoritmille voisin kuvitella kehitettävän yläsävelsarjaa hyödyntävän vastineen, rinnakkaisen algoritmin, joka perustuisi puhtaasti matemaattisiin suhteisiin toisin kuin K-K-systeemi. Se, olisiko sillä jotain yhteyttä havaintoon tai tonaalisesti suuntautuneeseen korvaan, on eri juttu. Myös Huronin konsonanssifunktion tapainen yläsävelsarjaan perustuva konsonoivuutta mittaava systeemi lienee mahdollinen (?)
Jos haluat laskea tasavireisen järjestelmän taajuudet (a1=440 Hz), ne saa oheisella funktiolla.
pitchfreq=function(n){27.5*2^((n-21)/12)}
Funktiolle annetaan syötteenä midisävelkorkeus. 27.5 Hz on alimman pianosta löytyvän sävelen taajuus. Taajuus kasvaa eksponentiaalisesti suhteessa puolisävelaskeliin tuollaisella kaavalla. Kokeile:
pitchfreq(60); # c1
pitchfreq(69); # a1
Jos haluat tulostaa kaikki pianosta löytyvät perustaajuudet, kokeile:
for(n in 21:108){print(pitchfreq(n))}
Oheinen kuva on luotu skriptillä, joka koettaa sovittaa yläsävelsarjaa annettuun sävelkorkeuksien joukkoon ja tulostaa tämän harmonian todennäköisen pohjasävelen. Funktiossa on vielä parantamisen varaa... Parsifal-alkusoitosta on laskettu tahtikohtaisesti pohjasävelet. Klikkaa kuvaa nähdäksesi sen suurempana.

Tuesday, April 25, 2006
Luento 28.4.2006
TARKENNUST OHJELMA:
Jaa mut juu ny onki sit miälenkiintost asiaa luvas ku Jop kertoo kui hää o analysoinu muutamii kansansävelmämelodioit tiatokoneel. Tehrääki nii, et mää lyhyest ota alux yhe näkökulma Henteli Messias-oratoorio teemoihi ja sit nautita toi Jopi juttu.
Messias_motiivit
***
Tää seuraava oli si vanhaa tiatoo:
Juu mää ajatteli iha alux hiukka vanhoi pikasest kerrat ja sit käyrä hiukka tota tilastotieret viel läpi samal taval ku viime kerral, sillee ärrää näpsytelle.
Ja sit pitäs päättä tehrääks perinteine tent vai ollaanx Henteli ääres hiukka pitemppä. Äänestettä siit sit viel.
Ja sit jos Jop viel esittele lyhykäisest sit skriptiäs.
Jaa mut juu ny onki sit miälenkiintost asiaa luvas ku Jop kertoo kui hää o analysoinu muutamii kansansävelmämelodioit tiatokoneel. Tehrääki nii, et mää lyhyest ota alux yhe näkökulma Henteli Messias-oratoorio teemoihi ja sit nautita toi Jopi juttu.
Messias_motiivit
***
Tää seuraava oli si vanhaa tiatoo:
Juu mää ajatteli iha alux hiukka vanhoi pikasest kerrat ja sit käyrä hiukka tota tilastotieret viel läpi samal taval ku viime kerral, sillee ärrää näpsytelle.
Ja sit pitäs päättä tehrääks perinteine tent vai ollaanx Henteli ääres hiukka pitemppä. Äänestettä siit sit viel.
Ja sit jos Jop viel esittele lyhykäisest sit skriptiäs.
Monday, April 17, 2006
Luennot 21.4.2006
Tein keinotekoisen aineiston, joukon lyhyitä vektoreita, jotka voisivat kuitenkin kuvata jotain musiikillista ominaisuutta. Teemme näistä kuvaajia, vertailemme ja järjestämme niitä eri tavoin. Kysymme, mitkä hahmot ovat keskenään samanlaisia ja millaisia ryhmiä muodostuu? Kyse on siis eräänlaisesta alkeellisesta hahmontunnistuksesta. Basic-juttu, mutta naputellessamme jotain jää selkärankaankin...
Skriptit täällä...
Näillä luennoilla käymme läpi R:ää naputellen. Tuon reference-card-monisteita mukanani, mutta jos niitä löytyy omasta takaa, ottakaa mukaan. Saamme professoristason vieraan 21.4. joten toivottavasti kaikki pääsevät skarppina mukaan ;-)
Skriptit täällä...
Näillä luennoilla käymme läpi R:ää naputellen. Tuon reference-card-monisteita mukanani, mutta jos niitä löytyy omasta takaa, ottakaa mukaan. Saamme professoristason vieraan 21.4. joten toivottavasti kaikki pääsevät skarppina mukaan ;-)
Thursday, April 06, 2006
Luento 7.4.2006

Jotain tuolla tuneR:lläkin voi tehdä???
Kurssia on vielä kolme kertaa jäljellä ja toivottavasti jonkinlainen haju on tullut siitä, mitä musiikintutkimuksen parissa tietokoneella voi esimerkiksi tehdä. En alun alkaenkaan asettanut mitään ehdottomia päämääriä, vaan lähdin liikkeelle sillä periaatteella, että katsotaan mitä ehditään. Artikkelin tekeminen on edelleenkin mahdollista ja sen voisi tehdä niin, että teen analysoitavat matskut ja skriptit valmiiksi analyysia varten ja sitten yhdessä tehdään pieni juttu niiden avulla. Sitä ei kuitenkaan ehdi yhden luennon aikana eikä ihan parinkaan vaan pitäisi viettää jokin kokonainen aamu- ja iltapäivä sen parissa. Jos sellaista halutaan, se sopii minulle.
Kahtena seuraavana kertana ajattelin kuitenkin keskittyä täysin R:n käyttöön, koska siitä saattaa olla nyt eniten hyötyä. Aikaisemmilla kerroilla on ollut esillä joitain mahdollisia lähestymistapoja, joiden pohjalta on toivottavasti syntynyt käsitys, että tietokone voi olla hyvinkin sopiva väline musiikintutkimukseen ja että se ei välttämättä ole niin monimutkaista, etteikö - ainakin konsultaation avittama - voisi joskus itsekin tehdä jotain tietokoneen kanssa.
Ajattelin 7.4. aluksi kerrata joitain asioita yhteenvedonomaisesti ja sen jälkeen testata hiukan tuneR-pakettia, joka on tehty äänenkäsittelyä varten. Itse en juuri tiedä äänen tutkimisesta oikeastaan mitään, mutta sehän ei toivottavasti menoa haittaa ;-) Jos JP, Juha, Jopi tai joku muu tietää jotain, älkää jättäkö kynttiläänne vakan alle. Ajattelin, että katsotaan tuneR-dokumentaatiota sillä silmällä, mitä se sisältää noin pääpiirteissään ja mitä siitä pystymme ymmärtämään. Wavista on kysymys ja jonkinlainen linkki paketissa näyttää olevan jopa lilypond-nuotinkirjoitusohjelmaan.
tuneR:n käyttö vaatii paketin lataamista koneelleen:
install.packages("tuneR") # tai sitten sieltä komentovalikosta graafisesti...
Brahmsin soittoa vaharullalta tuneR-testejä varten:
brahms2.wav
Wednesday, March 29, 2006
Luento 31.3.2006
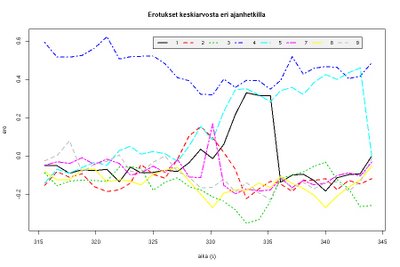
Juha R. esittelee hiukan omaa rytmiin liittyvää tutkimustaan ja sen pohjalta minä puolestani kerron plottaukseen eli kuvien piirtämiseen liittyvistä komennoista ja parametreista, regressiosuoran piirtämisestä, moniulotteisen skaalauksen tekemisestä R:llä ja jälleen kerran korrelaatiotesteistä. Keskihajontaakin tulee vielä hiukan demottua. Oheisen kuvan sisältökin selvinnee perjantaina. Kerrottakoon jo tässä vaiheessa, että siinä mm. ajanhetkellä 333 s kolmen koehenkilön komppi on kääntynyt upbeatiksi. Kuvaa klikkaamalla sen saa näkyviin suurempana.
Thursday, March 23, 2006
Luento 24.3.2006
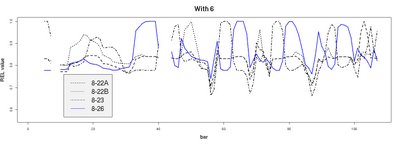 With 6. Blues mode 2 (21211212) merkattu sinisellä.
With 6. Blues mode 2 (21211212) merkattu sinisellä.Kiirettä pitää... mutta tässä blues mode2 -skripti alta löytyvän csv-fileen tutkimiseen.
Kokeilin nuita skriptejä yliopistolla tänään windowsissa ja nyt ne latautuvat ja toimivat. Testataan niiden käyttöä vielä Juhan transkription kohdalla. Tämän jälkeen jätetään joukkoteoria, jos ei kokonaan, niin ainakin joksikin aikaa. Sen erään Händel-motiivianalyysin olen ajatellut vielä toteuttaa...
Pidin tänään to 23.3. esitelmän ÅA:n symposiumissa "Sävellyksen harmonisen koherenssin mittaaminen vertailujoukkoanalyysin ja siirtymätodennäköisyysmatriisien avulla" ja voisin pikaisesti vilauttaa joitakin siihen liittyviä periaatteita, sillä aikaa kun nuo skriptit latautuvat koneille... Symposiumi jatkuu ja kannattaa katsoa, olisiko siellä jotakin kiinnostavaa. Osallistumismaksu on opiskelijoilta 5 e/pvä.
Tässä vielä laiton nuottikopio Juhan transkriptiosta...
Saturday, March 18, 2006
SetTheoryScripts again
Tein vielä erään lisäyksen kellokuva-skriptiin eli nyt se näyttää myös
Larry Solomonin taulukossaan (http://solomonsmusic.net/pcsets.htm)
esittämät joukkoluokkia karakterisoivat nimitykset.
Noin 37 kokeen jälkeen sain kuin sainkin tuon SetTheoryScripts-tiedoston
windowsissani toimimaan. En kyllä tiedä miksi. Kokeilin kaikenlaista,
erilaisia tekstikoodauksia tallennettaessa ja myös tallennuksia eri
ohjelmilla.
Nyt oheista liitteenä olevaa tiedostoa voisi kokeilla windowsissa. Mikäli
c-asemaan on lisäksi sijoitettu oheinen "4.csv" -tiedosto, sille tehdään
koodiin sisältyvät kokeet.
Ensin pitää kuitenkin ladata netistä grid- ja gtools -paketit komennoilla
install.packages("grid")
install.packages("gtools")
Sen jälkeen valitse File-valikosta komento "Source R code..." ja yllä linkistä
löytyvä tiedosto
"SetTheoryScripts"
Sen jälkeen kestää tovin - pieni kahvipaussi Euroshopper
persikka-passiohedelmä-jugurtin kera nautittuna (tällöin mikään ei ole
niin ihanaa kuin R-istunto) voi olla paikallaan - ennenkuin funktiot on
ajettu.
Tämän jälkeen voi katsoa komennolla
ls()
mitä funktioita onnistui ajamaan ja kokeilla vaikkapa funktiota pitchclock
tai rel2 luennolla esitellyllä tavalla, esim.:
X11(); pitchclock(c(4,8,3));
rel2("3-11A","3-11B");
Laitoin skripteihin funktioiden ajon jälkeen save.image() -komennon,
jolloin RData-nimiseen tiedostoon jonnekin R:n kansioissa jää nuo
muuttujat ja funktiot muistiin. Silloin seuraavan kerran, kun R
käynnistetään, ne latautuvat valmiiksi. Nyt kannattaa osallistua Tiinan
joukkoteoreettisille kursseille ja kerätä muutama opintopiste kotiin
tekemällä jokin yksinkertainen joukkoluokka-analyysi Schönbergin musiikista
tai mitä siellä käsitelläänkin...
Jostain syystä muutamat rivit ovat ilmeisesti windowsin R-editorille liian
pitkiä (joukkoluokkatiedot sisältävät rivit), minkä vuoksi funktioiden ajo
ei editorista copy-pastaamalla suoraan onnistu vaan pitää ottaa tuo
File-valikon "Source R code..."-komento. Kuitenkin Bach-analyysit
onnistuvat copy-pastaamallakin, jos ne keskeytyvät jostain syystä. Näin
kävi kerran itse kokeillessani ajoa.
lines()-komennon parametreihin ei näköjään saisi antaa y-akselille rajoja
tapaan "ylim=c(luku,luku)". Siitä johtuu muutama varoitus ajon aikana.
MacOSX- ja linux-käytössä pitää Bach-analyysin suorittamiseksi tsekata
oheiset polkumääritykset.
#MAC:
#Compo=read.table("/Users/4.csv",na.strings=".",header=F);
#attach(Compo);
t1=proc.time();
#LINUX:
#Compo=read.table("/home/atte/4.csv",na.strings=".",header=F);attach(Compo);
Tuesday, March 14, 2006
Luento 17.3.2006
Luennon materiaalia löytyy täältä:
TKAvustMusTutk060317.pdf
Lisäilin jotain ja korjailin hiukan noita joukkoteoriaskriptejä. Tein mm. sävelluokkakellon tuottavan algoritmin. Esimerkkinä kellokuva, jolle on annettu syötteenä oheinen vektori. Syötteenä funktiolle voi antaa sävelluokkia tai midisävelkorkeuksia. Sisällytin funktioon huvikseni Huronin konsonanssiarvonkin.
X11(); pitchclock(c(5,4,8,10,1,8,12));

Viimeksi jäi tuo joukkoteoreettinen analyysi esittelemättä ja ajattelin käydä hiukan läpi noita joukkoteoreettisia funktioita. Joukkoteorian perusteet eivät ole välttämättä kaikilla hanskassa, mutta sen avulla voi kuitenkin saada ihan ymmärrettäviä tuloksia.
Joukkoteoriaa käyttävät paitsi musiikkianalyytikot, myös säveltäjät yhä enenevässä määrin sen vuoksi, että nykyaikana harmonioita ei useinkaan pysty kategorisoimaan muulla tavoin kuin joukkoteoreettisesti. Kalev Tiits puhuu Musiikki-lehden 1-2/2005 numerossa artikkelissaan Hahmoetäisyyksien mittausmenetelmistä
aikasarjoissa ja musiikin vektoriesityksissä joukkoteorian "ajankohtaisuudesta" (s.64) varsin lämpimin sanoin.
Sävelluokkiin perustuvaan joukkoluokitukseen on koetettu kehittää myös laajennuksena sävelalat huomioonottavia teorioita. Tällaisia on Marcus Castrenin kehittämä "sointuluokitus". Tämä muistui mieleen siitä Jopin Huronin konsonanssifunktioon liittyvästä kritiikistä (mikä oli aivan oikeutettu). Konsonoivuuteenhan (ja sonoriteettiin?) vaikuttaa ennenkaikkea sävelten asema sävelalassa. Esim. kromaattisen klusterin sävelluokat tarpeeksi laajalle alueelle hajautettuna tai suhteessa bassoon riittävän korkealle asetettuina soivat paljon konsonoivammin kuin oktaavin sisään ahdettuna, joka Huronin intervalliluokkiin perustuvassa funktiossa on ikäänkuin oletuksena. Castrenin ratkaisun tapaan voisi kehittää myös tuota Huronin menetelmää tai niin, että sävelten suhde sitä alempien sävelten yläsävelsarjaan otettaisiin huomioon. Tässä jollekin elämäntehtävä.
Toisena tapauksena esittelen Huronin konsonanssifunktiolla tehdyn analyysin, joka kohdistuu melodiaan. Tämä taisi olla JP:n idea.
Melodian konsonoivuuden tutkimisesta tuli myös mieleen, että joku voisi joskus tutkia sitä, mitkä asiat vaikuttavat melodian solfaamisen vaikeuteen ja laulettavuuteen. Tietysti toiset intervallit ovat keskimäärin vaikeammin tuotettavissa kuin toiset (esim. tritonus on hankalampi laulaa kuin puhdas kvartti jne), mutta myös tonaalisella ympäristöllä on merkitystä. Jos melodian rytmi unohdetaan, voisi luoda Huronin konsonanssiprofiilin tyyppisen vektorin tai itse asiassa markovin ketjuilla asia onnistuisi paremmin, koska silloin voisi ottaa paremmin huomioon intervalleja ympäristössään, pitemmältä matkalta. Tällaisen matriisin luomiseksi tarvittaisiin monia kokeita vaikkapa solfaopiskelijoiden keskuudessa. Laulatettaisiin monia erilaisia melodioita ja virhepaikat merkattaisiin muistiin (+ tietty määrä sitä edeltäviä intervalleja). Kun matriisi olisi luotu, voitaisiin laskea vaikkapa Modus novus- opuksen kullekin melodialle vaikeusaste:-)
JP kyseli tyyppiarvon eli moodin tuottavaa funktiota R:ssä. En löytänyt sellaista, mutta kyseessähän on tunnusluku, joka kuvaa sitä, mitä arvoa muuttujassa on eniten. Sen saa esimerkiksi näin:
tyyppiarvo <- function(vektori)
{
frekvenssitaulukko=table(vektori)
maxmaara=max(frekvenssitaulukko)
lukuarvo=as.double(names(frekvenssitaulukko[rev(order(table(vektori)))[1]]))
return(list(lukuarvo=lukuarvo, maxmaara=maxmaara))
}
eli kuinka paljon tiettyä lukua on enimmillään saadaan siten, että vektorin luvuista muodostetaan frekvenssitaulukko (table), josta lasketaan maksimifrekvenssi. Tämä sijoitetaan muuttujaan "maxmaara". Itse tyyppiarvoa varten täytyy frekvenssitaulukko järjestää frekvenssien mukaan (order). Sen jälkeen käännetään (rev) tulos, niin että se indeksi, joka on saanut eniten osumia, tulee ensimmäiseksi ja lopuksi poimitaan (names-komento ei poimi itse frekvenssiä vaan nimenomaan sen luvun, johon suurin frekvenssi liittyy, ikäänkuin rivin "nimen") tuo indeksillä 1 oleva luku ([1]). Tässä hiukan kehitin tuota funktiota niin, että nyt voidaan kutsua jompaa kumpaa
esim:
1) jos halutaan tyyppiarvon esiintymisten lukumäärä:
tyyppiarvo(c(6,5.5,4,5.5,4,2))$maxmaara
2) jos halutaan itse tyyppiarvo
tyyppiarvo(c(6,5.5,4,5.5,4,2))$lukuarvo
Midicsv:n antamien taulukoiden muokkaaminen R:ssä toimivaan muotoon vaatii aikalailla työtä. Löysin taas sellaisen midimuodon, joka vaatii omanlaistansa käsittelyä. Toimivan funktion luomisesta voi tulla pidempi projekti, mutta kuten Jopi totesi, jotta pääsisimme heti hommiin käsiksi, pitäisi tällainenkin R:ssä olla. Polyfoniset midit vaativat sitten oman käsittelyn, mutta kunhan saamme turhat röhnät pois, voisi luoda funktioita, jotka muokkaavat taulukon sopivaan muotoon erityyppisiä lähestymistapoja varten.
TKAvustMusTutk060317.pdf
Lisäilin jotain ja korjailin hiukan noita joukkoteoriaskriptejä. Tein mm. sävelluokkakellon tuottavan algoritmin. Esimerkkinä kellokuva, jolle on annettu syötteenä oheinen vektori. Syötteenä funktiolle voi antaa sävelluokkia tai midisävelkorkeuksia. Sisällytin funktioon huvikseni Huronin konsonanssiarvonkin.
X11(); pitchclock(c(5,4,8,10,1,8,12));

Viimeksi jäi tuo joukkoteoreettinen analyysi esittelemättä ja ajattelin käydä hiukan läpi noita joukkoteoreettisia funktioita. Joukkoteorian perusteet eivät ole välttämättä kaikilla hanskassa, mutta sen avulla voi kuitenkin saada ihan ymmärrettäviä tuloksia.
Joukkoteoriaa käyttävät paitsi musiikkianalyytikot, myös säveltäjät yhä enenevässä määrin sen vuoksi, että nykyaikana harmonioita ei useinkaan pysty kategorisoimaan muulla tavoin kuin joukkoteoreettisesti. Kalev Tiits puhuu Musiikki-lehden 1-2/2005 numerossa artikkelissaan Hahmoetäisyyksien mittausmenetelmistä
aikasarjoissa ja musiikin vektoriesityksissä joukkoteorian "ajankohtaisuudesta" (s.64) varsin lämpimin sanoin.
Sävelluokkiin perustuvaan joukkoluokitukseen on koetettu kehittää myös laajennuksena sävelalat huomioonottavia teorioita. Tällaisia on Marcus Castrenin kehittämä "sointuluokitus". Tämä muistui mieleen siitä Jopin Huronin konsonanssifunktioon liittyvästä kritiikistä (mikä oli aivan oikeutettu). Konsonoivuuteenhan (ja sonoriteettiin?) vaikuttaa ennenkaikkea sävelten asema sävelalassa. Esim. kromaattisen klusterin sävelluokat tarpeeksi laajalle alueelle hajautettuna tai suhteessa bassoon riittävän korkealle asetettuina soivat paljon konsonoivammin kuin oktaavin sisään ahdettuna, joka Huronin intervalliluokkiin perustuvassa funktiossa on ikäänkuin oletuksena. Castrenin ratkaisun tapaan voisi kehittää myös tuota Huronin menetelmää tai niin, että sävelten suhde sitä alempien sävelten yläsävelsarjaan otettaisiin huomioon. Tässä jollekin elämäntehtävä.
Toisena tapauksena esittelen Huronin konsonanssifunktiolla tehdyn analyysin, joka kohdistuu melodiaan. Tämä taisi olla JP:n idea.
Melodian konsonoivuuden tutkimisesta tuli myös mieleen, että joku voisi joskus tutkia sitä, mitkä asiat vaikuttavat melodian solfaamisen vaikeuteen ja laulettavuuteen. Tietysti toiset intervallit ovat keskimäärin vaikeammin tuotettavissa kuin toiset (esim. tritonus on hankalampi laulaa kuin puhdas kvartti jne), mutta myös tonaalisella ympäristöllä on merkitystä. Jos melodian rytmi unohdetaan, voisi luoda Huronin konsonanssiprofiilin tyyppisen vektorin tai itse asiassa markovin ketjuilla asia onnistuisi paremmin, koska silloin voisi ottaa paremmin huomioon intervalleja ympäristössään, pitemmältä matkalta. Tällaisen matriisin luomiseksi tarvittaisiin monia kokeita vaikkapa solfaopiskelijoiden keskuudessa. Laulatettaisiin monia erilaisia melodioita ja virhepaikat merkattaisiin muistiin (+ tietty määrä sitä edeltäviä intervalleja). Kun matriisi olisi luotu, voitaisiin laskea vaikkapa Modus novus- opuksen kullekin melodialle vaikeusaste:-)
JP kyseli tyyppiarvon eli moodin tuottavaa funktiota R:ssä. En löytänyt sellaista, mutta kyseessähän on tunnusluku, joka kuvaa sitä, mitä arvoa muuttujassa on eniten. Sen saa esimerkiksi näin:
tyyppiarvo <- function(vektori)
{
frekvenssitaulukko=table(vektori)
maxmaara=max(frekvenssitaulukko)
lukuarvo=as.double(names(frekvenssitaulukko[rev(order(table(vektori)))[1]]))
return(list(lukuarvo=lukuarvo, maxmaara=maxmaara))
}
eli kuinka paljon tiettyä lukua on enimmillään saadaan siten, että vektorin luvuista muodostetaan frekvenssitaulukko (table), josta lasketaan maksimifrekvenssi. Tämä sijoitetaan muuttujaan "maxmaara". Itse tyyppiarvoa varten täytyy frekvenssitaulukko järjestää frekvenssien mukaan (order). Sen jälkeen käännetään (rev) tulos, niin että se indeksi, joka on saanut eniten osumia, tulee ensimmäiseksi ja lopuksi poimitaan (names-komento ei poimi itse frekvenssiä vaan nimenomaan sen luvun, johon suurin frekvenssi liittyy, ikäänkuin rivin "nimen") tuo indeksillä 1 oleva luku ([1]). Tässä hiukan kehitin tuota funktiota niin, että nyt voidaan kutsua jompaa kumpaa
esim:
1) jos halutaan tyyppiarvon esiintymisten lukumäärä:
tyyppiarvo(c(6,5.5,4,5.5,4,2))$maxmaara
2) jos halutaan itse tyyppiarvo
tyyppiarvo(c(6,5.5,4,5.5,4,2))$lukuarvo
Midicsv:n antamien taulukoiden muokkaaminen R:ssä toimivaan muotoon vaatii aikalailla työtä. Löysin taas sellaisen midimuodon, joka vaatii omanlaistansa käsittelyä. Toimivan funktion luomisesta voi tulla pidempi projekti, mutta kuten Jopi totesi, jotta pääsisimme heti hommiin käsiksi, pitäisi tällainenkin R:ssä olla. Polyfoniset midit vaativat sitten oman käsittelyn, mutta kunhan saamme turhat röhnät pois, voisi luoda funktioita, jotka muokkaavat taulukon sopivaan muotoon erityyppisiä lähestymistapoja varten.
Thursday, March 09, 2006
Luento 10.3.2006
Laitoin utu:n palvelimelle muutamia musiikin joukkoteoriaan liittyviä skriptejä, jotka voi ladata tästä linkistä.
Demotiedosto em. skriptien testaukseen:
J.S.Bach: Es ist genug 4.csv.
Käyn 10.3. läpi muutamia tenttiin liittyviä asioita ja toivon, että sen jälkeen syntyisi keskustelua II periodin tavoitteista. Ehdotin siis yhteisiin alijonoihin, markovin ketjuihin ja joukkoteoriaan liittyviä lähestymistapoja, niitä kun on ollut jo aikaisemmin esille. Koska näitäkin voi soveltaa niin monella tavalla, voisimme keskustella siitä, millaiseen aineistoon näitä soveltaisimme ja millaisiin parametreihin. Nuo joukkoteoriaskriptit on tuossa siltäkin varalta, että aikaa jää hiukan niiden testaamiseen.
Testaaminen vaatii paketin gtools-asentamista komennolla
install.packages("gtools")
ja tietysti toimivaa verkkoyhteyttä. OSX:ssä voi käyttää valikkokomentoa "Package Installer".
Kun oheisen 4.csv -tiedoston sijoittaa Windows-koneessa c-hakemistoon, voi koko skriptin ajaa kerralla ilman pahempia virheilmoituksia, muutoin latautuvat vain alkupuolen funktiot, mutta Bach-analyysi jää tekemättä (jos sijoittaa csv-tiedoston muualle koneeseen, täytyy read.table-komentoon liittyvä polku muokata sen mukaan, ohjelmalistauksessa puolen välin jälkeen "SOME SAMPLE SCRIPTS"-kohdan alla. Systeemistä riippuen täytyy #-merkki poistaa kyseisen "Compo=read.table(...)" -komennon edestä. Tällöin ko. skripti ajetaan.) Se viekin tovin, ennenkuin koko ohjelma funktioineen on ajettu. Joukossa on pari print-komentoa, jotka hiukan hidastavat lataamista, mutta joiden avulla toisaalta voi seurata tapahtumien kulkua.
No, demoan tätä luennolla, jos aikaa jää.
Demotiedosto em. skriptien testaukseen:
J.S.Bach: Es ist genug 4.csv.
Käyn 10.3. läpi muutamia tenttiin liittyviä asioita ja toivon, että sen jälkeen syntyisi keskustelua II periodin tavoitteista. Ehdotin siis yhteisiin alijonoihin, markovin ketjuihin ja joukkoteoriaan liittyviä lähestymistapoja, niitä kun on ollut jo aikaisemmin esille. Koska näitäkin voi soveltaa niin monella tavalla, voisimme keskustella siitä, millaiseen aineistoon näitä soveltaisimme ja millaisiin parametreihin. Nuo joukkoteoriaskriptit on tuossa siltäkin varalta, että aikaa jää hiukan niiden testaamiseen.
Testaaminen vaatii paketin gtools-asentamista komennolla
install.packages("gtools")
ja tietysti toimivaa verkkoyhteyttä. OSX:ssä voi käyttää valikkokomentoa "Package Installer".
Kun oheisen 4.csv -tiedoston sijoittaa Windows-koneessa c-hakemistoon, voi koko skriptin ajaa kerralla ilman pahempia virheilmoituksia, muutoin latautuvat vain alkupuolen funktiot, mutta Bach-analyysi jää tekemättä (jos sijoittaa csv-tiedoston muualle koneeseen, täytyy read.table-komentoon liittyvä polku muokata sen mukaan, ohjelmalistauksessa puolen välin jälkeen "SOME SAMPLE SCRIPTS"-kohdan alla. Systeemistä riippuen täytyy #-merkki poistaa kyseisen "Compo=read.table(...)" -komennon edestä. Tällöin ko. skripti ajetaan.) Se viekin tovin, ennenkuin koko ohjelma funktioineen on ajettu. Joukossa on pari print-komentoa, jotka hiukan hidastavat lataamista, mutta joiden avulla toisaalta voi seurata tapahtumien kulkua.
No, demoan tätä luennolla, jos aikaa jää.
Thursday, March 02, 2006
Thursday, February 23, 2006
Friday, February 17, 2006
Nth order markov music analysis and generation
Ohessa n:nnen kertaluvun markov-skripti sekä analyysia että musiikin generoimista varten. Koetan selkeyttää sitä vielä tästä, mutta laitanpahan sen sellaisena kuin se on nyt, kun asiasta oli puhetta luennolla. Olen käyttänyt lisp-tulkkia ja nk. "Cope events"-muotoista listaa R:stä saatujen generointien kääntämiseksi midi-muotoon ja kääntänyt Finalella vielä miditiedoston nuotiksi, mutta täytyypi tutkia, mitä tuo csvmidi-ohjelma vaatii toimiakseen. Seuraavaksi täytyy vielä selvittää, miten midicsv:n kääntämästä tiedostosta saadaan rytmit ulos.
NthOrdMarkovAnalAndComp
NthOrdMarkovAnalAndComp
Wednesday, February 15, 2006
Miditiedon tuominen R:ään windowsissa ja OSX:ssä
Oheisessa skriptissä on ohjeet, kuinka midicsv-ohjelma asennetaan windowsiin ja mac OSX:ään sekä kuinka midi-tiedosto muutetaan csv-muotoon ja miten tämä taulukko taas tuodaan R:ään. Olen käyttänyt oletushakemistona windowsin tapauksessa c-asemaa, mutta se voi olla tietysti jokin ihan muu, kunhan tämä otetaan huomioon skripteissä.
midi2R
midi2R
6. luento 17.2.2006
Tällä luennolla demonstroin mm. for-silmukan ja if-ehtorakenteen käyttöä .
Luentokalvot löytyvät tästä:
TKAvustMusTutk060217b
Oheisella ohjelmalla verrataan sävellysten melodiaintervalleista muodostettujen siirtymätodennäköisyysmatriisien samankaltaisuutta nk. euklidisen etäisyysmitan avulla. Otoksessa on 3 irlantilaista ja 3 suomalaista kansantanssia. Eli tässä käytetään aikaisemmin esiteltyjä markovin ketjuja siirtymätodennäköisyysmatriisien muodostamiseen.
Kansantanssitiedostot csv-taulukkoina. Zip-pakattu tiedosto.
Nämä midit on haettu seuraavilta sivuilta:
Irlantilaiset:
http://tadpole.mytunebook.de/tunes/celtmidi/celtic.htm
1) Staten Island.
2) Tenpenny Bit.
3) The Fiddler is Drunk from the playing of Sean Keane (fiddle).
Suomalaiset:
http://www.jyu.fi/musica/sks/collection_download.html
1) kt1_0057.mid
2) kt1_0101.mid
3) kt1_0613.mid
Skripti löytyy tästä:
6_luennon_skripti
Käymme sen luennolla läpi vaihe vaiheelta.
Mittaus on hyvin karkea. Ensinnäkin tässä käytetään 1. kertaluvun markovketjua ja toiseksi parametreista on valittu ainoastaan sävelkorkeudet tai tarkemmin, niiden väliset intervallit. Rytmiparametri on tyystin unohdettu. Midifileiden kanssa täytyy olla tarkkana. Tein ensin väärät laskelmat, koska tiedostot olivat koodatut eri tavoin. Syötin kaikki Finale-ohjelman läpi ja nyt skriptit toimivat.
Suomalaisista sävelmistä sävelmät 1 ja 2 olivat mollisävelmiä. Muut otoksessa ovat duurisävelmiä. 3. suomalaisista sävelmistä on parasta pataa kaikkien kanssa ja sen sekä 1. irlantilaissävelmän etäisyys on pienin. Se edustaa jonkinlaista keskiarvoa joukossa. Sen etäisyys 1. suomalaismelodiaan on myös suhteessa pieni, vaikka tämä kulkeekin mollissa.
Tulostaulukko kuvassa:

Luentokalvot löytyvät tästä:
TKAvustMusTutk060217b
Oheisella ohjelmalla verrataan sävellysten melodiaintervalleista muodostettujen siirtymätodennäköisyysmatriisien samankaltaisuutta nk. euklidisen etäisyysmitan avulla. Otoksessa on 3 irlantilaista ja 3 suomalaista kansantanssia. Eli tässä käytetään aikaisemmin esiteltyjä markovin ketjuja siirtymätodennäköisyysmatriisien muodostamiseen.
Kansantanssitiedostot csv-taulukkoina. Zip-pakattu tiedosto.
Nämä midit on haettu seuraavilta sivuilta:
Irlantilaiset:
http://tadpole.mytunebook.de/tunes/celtmidi/celtic.htm
1) Staten Island.
2) Tenpenny Bit.
3) The Fiddler is Drunk from the playing of Sean Keane (fiddle).
Suomalaiset:
http://www.jyu.fi/musica/sks/collection_download.html
1) kt1_0057.mid
2) kt1_0101.mid
3) kt1_0613.mid
Skripti löytyy tästä:
6_luennon_skripti
Käymme sen luennolla läpi vaihe vaiheelta.
Mittaus on hyvin karkea. Ensinnäkin tässä käytetään 1. kertaluvun markovketjua ja toiseksi parametreista on valittu ainoastaan sävelkorkeudet tai tarkemmin, niiden väliset intervallit. Rytmiparametri on tyystin unohdettu. Midifileiden kanssa täytyy olla tarkkana. Tein ensin väärät laskelmat, koska tiedostot olivat koodatut eri tavoin. Syötin kaikki Finale-ohjelman läpi ja nyt skriptit toimivat.
Suomalaisista sävelmistä sävelmät 1 ja 2 olivat mollisävelmiä. Muut otoksessa ovat duurisävelmiä. 3. suomalaisista sävelmistä on parasta pataa kaikkien kanssa ja sen sekä 1. irlantilaissävelmän etäisyys on pienin. Se edustaa jonkinlaista keskiarvoa joukossa. Sen etäisyys 1. suomalaismelodiaan on myös suhteessa pieni, vaikka tämä kulkeekin mollissa.
Tulostaulukko kuvassa:

Friday, February 10, 2006
4 kertaluvun markov-generointi J.S. Bachin Prestosta sooloviululle
Kokeilin 3. ja 4. kertaluvun markov-ketjuja generoidakseni J.S. Bachin sooloviulusävellyksen pohjalta uusia "Prestoja".
Ohessa kolme "ajoa":
3. kertaluvun sävellys
4. kertaluvun sävellys 1
4. kertaluvun sävellys 2
Bachin alkuperäinen sävellys.
Algoritmi on siis tehty R:llä. Sitten olen muuttanut saadun sävelvektorin nk. Cope-tapahtumiksi (Cope-events) ja lispillä tuottanut midi-versiot.
Ohessa kolme "ajoa":
3. kertaluvun sävellys
4. kertaluvun sävellys 1
4. kertaluvun sävellys 2
Bachin alkuperäinen sävellys.
Algoritmi on siis tehty R:llä. Sitten olen muuttanut saadun sävelvektorin nk. Cope-tapahtumiksi (Cope-events) ja lispillä tuottanut midi-versiot.
Wednesday, February 08, 2006
5. luento 10.2.2006
Ohessa ppt-kalvot pdf:nä
TKAvustMusTutk060210.pdf
sekä Olli Linjaman improvisaatio nro 756 csv-taulukkona.
Tällä kerralla "pelataan", sehän se on tietokoneiden alkuperäinen käyttötarkoituskin ;-)
Eli käymme läpi R:n komentoja, mekaanisesti, näpyttelyharjoituksen tapaan, pääosin mallin mukaan. Vähemmän ajattelua, enemmän tekemistä! Mukana on uutta ja vanhaa. Muuta emme sitten teekään, vaan käytämme kaiken aikamme näpyttelemiseen, jotta R tulisi vähitellen käytännön kokemusten kautta tutuksi. Vaikka ohjelmoiminen ei olekaan kurssin pääsisältö ja tarkoitus, se on hyödyllinen taito ja musiikkianalyysejä tehtäessä välttämätön. Kun II periodilla teemme pari laajempaa analyysityötä, on hyvä tietää, mitä ohjelmarivit ainakin suurinpiirtein tekevät. Ja R:äähän voi käyttää tietysti myös muuhun kuin musiikkiaineiston tutkimiseen ja analyysiin (esim. kyselytulosten tai vaikkapa tekstin analyysiin). Muut (kuin muusikot) pääsevät usein helpommalla, koska R:stä löytyy suoraan tilastolaskentaan valtavasti valmiita funktioita, kunhan vain tutkittava aineistotaulukko on valmiina.
6. kerralla teemme pari ohjelmaa, joissa tarvitaan peräkkäis-, valinta- ja toistorakenteita.
TKAvustMusTutk060210.pdf
sekä Olli Linjaman improvisaatio nro 756 csv-taulukkona.
Tällä kerralla "pelataan", sehän se on tietokoneiden alkuperäinen käyttötarkoituskin ;-)
Eli käymme läpi R:n komentoja, mekaanisesti, näpyttelyharjoituksen tapaan, pääosin mallin mukaan. Vähemmän ajattelua, enemmän tekemistä! Mukana on uutta ja vanhaa. Muuta emme sitten teekään, vaan käytämme kaiken aikamme näpyttelemiseen, jotta R tulisi vähitellen käytännön kokemusten kautta tutuksi. Vaikka ohjelmoiminen ei olekaan kurssin pääsisältö ja tarkoitus, se on hyödyllinen taito ja musiikkianalyysejä tehtäessä välttämätön. Kun II periodilla teemme pari laajempaa analyysityötä, on hyvä tietää, mitä ohjelmarivit ainakin suurinpiirtein tekevät. Ja R:äähän voi käyttää tietysti myös muuhun kuin musiikkiaineiston tutkimiseen ja analyysiin (esim. kyselytulosten tai vaikkapa tekstin analyysiin). Muut (kuin muusikot) pääsevät usein helpommalla, koska R:stä löytyy suoraan tilastolaskentaan valtavasti valmiita funktioita, kunhan vain tutkittava aineistotaulukko on valmiina.
6. kerralla teemme pari ohjelmaa, joissa tarvitaan peräkkäis-, valinta- ja toistorakenteita.
Wednesday, February 01, 2006
Luennoista 5.-7.
5. kerraksi olen ajatellut, että kävisimme järjestelmällisesti läpi R:n funktioita käsityönä eli referenssikortteja ja tietokoneita käyttäen ja 6. luennolla tekisimme funktioita ja harjoittelisimme edellistunnin tapaan ohjelman ääressä silmukoiden ja ehtolauseiden kirjoittamista. Molemmilla kerroilla skriptit kirjoitetaan ensin R:n editoriin ja sitten testataan komentoja R:n komentorivillä. Kirjoitetut skriptit myös tallennetaan tekstidokumentiksi suoraan editorista.
7. luennolla ennen tenttiä keskustelemme aluksi tulevista projekteista ja lyömme lukkoon käytettävät materiaalit ja lähestymistavat (menetelmät saattavat tietysti vielä 2. periodilla kehittyä ja muuttua) ja jos aikaa sitten jää, käyttäisimme sen R:n opiskeluun.
Tenttisuorituksena 3.3. olen ajatellut, että annan muutamia lyhyitä tehtäviä peräkkäisrakenteeseen, valintarakenteeseen ja toistorakenteeseen liittyen, kuitenkin niin, että syvällisiä tilastollisia tietoja ei tarvita ja siten, että niin referenssikortteja kuin tietysti R:n helppiä saa käyttää (R:ssä siis: help() tai ?komento). Tentin tarkoitus on ennen kaikkea kartoittaa sitä, mitä olette oppineet ja ymmärtäneet, jotta osaan sitten jatkossa paikata ja suunnata opetusta tarvittaessa.
7. luennolla ennen tenttiä keskustelemme aluksi tulevista projekteista ja lyömme lukkoon käytettävät materiaalit ja lähestymistavat (menetelmät saattavat tietysti vielä 2. periodilla kehittyä ja muuttua) ja jos aikaa sitten jää, käyttäisimme sen R:n opiskeluun.
Tenttisuorituksena 3.3. olen ajatellut, että annan muutamia lyhyitä tehtäviä peräkkäisrakenteeseen, valintarakenteeseen ja toistorakenteeseen liittyen, kuitenkin niin, että syvällisiä tilastollisia tietoja ei tarvita ja siten, että niin referenssikortteja kuin tietysti R:n helppiä saa käyttää (R:ssä siis: help() tai ?komento). Tentin tarkoitus on ennen kaikkea kartoittaa sitä, mitä olette oppineet ja ymmärtäneet, jotta osaan sitten jatkossa paikata ja suunnata opetusta tarvittaessa.
Friday, January 27, 2006
4. luento 3.2.2006
Neljännen luennon ppt-kalvot löytyvät tästä
TKAvustMusTutk060203b.pdf. (b-versio...)
Sävelluokkajoukosta intervalliluokkavektorin laskeva skripti löytyy tästä:
icv_skripti.rtf
Saman asian voisi tehdä tyylikkäämmin, mutta jos joku haluaa kokeilla, voi ajaa funktion "icv2" R:ään ja sitten kokeilla kirjoittaa komentoriville jotain tämän tapaista:
icv2(c(0,4,7,10,4,0,7))
ja saa tulokseksi C-dominanttiseptimisoinnun intervalliluokkavektorin.
* * *
Ensi kerrasta lähtien koetan edetä hiukan lunkimmin... Tutustumme funktion tekemiseen ja ajattelin, että malliksi voisimme luoda funktion, joka laskee yksinkertaisella periaatteella sävelluokkien perusteella tonaalisuusarvioita. Tällainen funktio vaatii muutaman rivin, ei enempää. Voimme käyttää siinä apunamme nk. Krumhansl-Kessler -profiileja (joihin Jopi viittasi tunnin jälkeen... ;-)
Joku voisikin tehdä sointuanalyysin Solagen sävellyksestä, jos saa sen käsiinsä jostain?
Tässä linkki Juhan mainitsemaan artikkeliin, jossa Coltranen improvisaatioita on analysoitu markovin ketjujen avulla.
http://scholar.lib.vt.edu/theses/available/etd-61098-131249/unrestricted/dmfetd.pdf
Teksti on laaja, mutta koetan perehtyä siihen heti kun ehdin. Ohessa pari linkkiä lyhyisiin teksteihin, joista käy ilmi, että markovin ketjujen soveltaminen musiikin analysoimiseen on periaatteiltaan sinänsä melko yksinkertainen ja selkeä juttu.
http://www.music-cog.ohio-state.edu/Music829D/Notes/Infotheory.html
http://journal-ci.csse.monash.edu.au/ci/vol03/mccorm/mccorm.html
Etenkin tästä jälkimmäisestä linkistä löytyvän tekstin luvussa "Representations for Music Composition" ja sen alaluvussa "Markov Models "on havainnollinen kuva siitä, mistä markovin ketjuissa on kysymys. Esimerkkinä on melodian "Maijal oli karitsa" pohjalta tehty nk. "siirtymätodennäköisyysmatriisi". Kyseessä on ns. "1st order model". En ole tällä periaatteella musiikkia juurikaan analysoinut (yhtä lyhyttä Kalifornian keikkaa lukuunottamatta), mutta minua kiinnostaisi tehdä analyyseja esim. eri säveltäjien melodioiden pohjalta ja sitten jollain "etäisyysmitalla" verrata syntyviä siirtymätodennäköisyysmatriiseja. Palaan tähän asiaan seuraavalla luennolla. Jos ehditte ja jota kiinnostaa, lukekaa tuo jälkimmäinen artikkeli. Se ei ole pitkä. Jo pelkästään tuon mainitsemani kuvan tarkasteleminen saattaa tehdä idean selväksi. Kyseisessä tekstissä puhutaan lähinnä algoritmisesta säveltämisestä, jota edeltää tietyn tyylisen musiikin analyysi. Markovin ketjujen avulla pystytään tuottamaan samantyylistä musiikkia. Kyseessä on yksi eniten käytetyistä keinoista algoritmisen säveltämisen piirissä. Me voisimme keskittyä tässä vaiheessa vain analyysiin...
Tälle sivulle voi kirjoittaa kommenttejaan klikkaamalla Comments-tekstiä näiden kirjoitusten lopussa, kynä-symbolin vieressä.
TKAvustMusTutk060203b.pdf. (b-versio...)
Sävelluokkajoukosta intervalliluokkavektorin laskeva skripti löytyy tästä:
icv_skripti.rtf
Saman asian voisi tehdä tyylikkäämmin, mutta jos joku haluaa kokeilla, voi ajaa funktion "icv2" R:ään ja sitten kokeilla kirjoittaa komentoriville jotain tämän tapaista:
icv2(c(0,4,7,10,4,0,7))
ja saa tulokseksi C-dominanttiseptimisoinnun intervalliluokkavektorin.
* * *
Ensi kerrasta lähtien koetan edetä hiukan lunkimmin... Tutustumme funktion tekemiseen ja ajattelin, että malliksi voisimme luoda funktion, joka laskee yksinkertaisella periaatteella sävelluokkien perusteella tonaalisuusarvioita. Tällainen funktio vaatii muutaman rivin, ei enempää. Voimme käyttää siinä apunamme nk. Krumhansl-Kessler -profiileja (joihin Jopi viittasi tunnin jälkeen... ;-)
Joku voisikin tehdä sointuanalyysin Solagen sävellyksestä, jos saa sen käsiinsä jostain?
Tässä linkki Juhan mainitsemaan artikkeliin, jossa Coltranen improvisaatioita on analysoitu markovin ketjujen avulla.
http://scholar.lib.vt.edu/theses/available/etd-61098-131249/unrestricted/dmfetd.pdf
Teksti on laaja, mutta koetan perehtyä siihen heti kun ehdin. Ohessa pari linkkiä lyhyisiin teksteihin, joista käy ilmi, että markovin ketjujen soveltaminen musiikin analysoimiseen on periaatteiltaan sinänsä melko yksinkertainen ja selkeä juttu.
http://www.music-cog.ohio-state.edu/Music829D/Notes/Infotheory.html
http://journal-ci.csse.monash.edu.au/ci/vol03/mccorm/mccorm.html
Etenkin tästä jälkimmäisestä linkistä löytyvän tekstin luvussa "Representations for Music Composition" ja sen alaluvussa "Markov Models "on havainnollinen kuva siitä, mistä markovin ketjuissa on kysymys. Esimerkkinä on melodian "Maijal oli karitsa" pohjalta tehty nk. "siirtymätodennäköisyysmatriisi". Kyseessä on ns. "1st order model". En ole tällä periaatteella musiikkia juurikaan analysoinut (yhtä lyhyttä Kalifornian keikkaa lukuunottamatta), mutta minua kiinnostaisi tehdä analyyseja esim. eri säveltäjien melodioiden pohjalta ja sitten jollain "etäisyysmitalla" verrata syntyviä siirtymätodennäköisyysmatriiseja. Palaan tähän asiaan seuraavalla luennolla. Jos ehditte ja jota kiinnostaa, lukekaa tuo jälkimmäinen artikkeli. Se ei ole pitkä. Jo pelkästään tuon mainitsemani kuvan tarkasteleminen saattaa tehdä idean selväksi. Kyseisessä tekstissä puhutaan lähinnä algoritmisesta säveltämisestä, jota edeltää tietyn tyylisen musiikin analyysi. Markovin ketjujen avulla pystytään tuottamaan samantyylistä musiikkia. Kyseessä on yksi eniten käytetyistä keinoista algoritmisen säveltämisen piirissä. Me voisimme keskittyä tässä vaiheessa vain analyysiin...
Tälle sivulle voi kirjoittaa kommenttejaan klikkaamalla Comments-tekstiä näiden kirjoitusten lopussa, kynä-symbolin vieressä.
Sävelnimet sävelluokiksi ja midisävelkorkeuksiksi
Oheisessa tekstitiedostossa vielä luentokalvoilla ollut skripti, jonka piti muuttaa sävelnimet sävelluokiksi ja midisävelkorkeuksiksi ja "hiukan" pidempi, mutta periaatteiltaan paljon yksinkertaisempi skripti samaan hommaan, jos copy-pastaaminen ei onnistu suoraan pdf:stä. Tästä se näyttäisi onnistuvan molemmilla vaihtoehdoilla.
V4_skripti
Ohessa vielä kommentit tuohon monimutkaiseen, tiiviiseen skriptiin.
V4 skriptin selitys
V4_skripti
Ohessa vielä kommentit tuohon monimutkaiseen, tiiviiseen skriptiin.
V4 skriptin selitys
Thursday, January 26, 2006
3. luento 27.1.2006
Seuraavan luennon ppt-kalvot pdf:nä
TKAvustMusTutk060127.pdf
Ohessa linkki tiedostoon, jota käsittelemme tunnilla. Kyseessä on Solage-nimisen säveltäjän teoksesta Fumeux fumes irrotettu diskanttimelodia.
fumeux_sopr.csv
Säveltäjä kuuluu ns. Ars Subtilior -kouluun 1300 luvulla. Aika hienoa musiikkia!
http://www.pacificnet.net/~garyrich/subtilior/
Tällä luennolla käyn läpi tilastotieteeseen liittyviä asioita ja käsitteitä - vauhdilla... Tarkoituksenani on, että tilastomenetelmistä ja niiden tarjoamista mahdollisuuksista jäisi jonkinlainen haju (tai - toivottavasti - paremminkin tuoksu ;-).
Tämän luentokerran jälkeen otetaan hiukan rauhallisemmin ja katsotaan, mihin suuntaan lähdetään. Keskitymme yhä enemmän R:n opiskeluun ja sovelluksiin, mutta välillä palaamme tilastojen ja tarvittaessa joukkoteorian pariin. Ja kuten tulette huomaamaan, kertaan samoja R:n komentojakin uudelleen ja uudelleen.
Mielessä on käynyt, että voisimme lähestyä kevään analyyseja esimerkiksi kahdella tavalla, markovin ketjuja hyödyntäen ja joukkoteoriaa käyttäen. Molemmat metodit ovat musiikkitieteessä käypiä eivätkä liian kuluneita, päin vastoin. Mutta muitakin tapoja varmasti keksimme ja saa ehdottaa ja niistä voisimme keskustella neljännen luentokerran jälkipuolella. Ajattelin 4. kerralla aloittaa siitä, miten R:ssä luodaan omia funktioita ja kuinka toistorakenteita (looppeja) ja ehtorakenteita R:ssä kirjoitetaan.
3. luentokalvoissa esitettyjen skriptien lopussa saadaan seuraavanlainen kuvaaja Fumeux fumes -melodiasta, josta nähdään, että se koostuu kuudesta kaarroksesta.
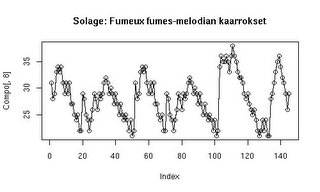
Laitoinpa tähän vielä linkin midi-tiedostoon musiikin kuuntelusta nauttivien iloksi!
Fumeux fumes
Erään biisin basso
EraanBiisinBasso.csv
TKAvustMusTutk060127.pdf
Ohessa linkki tiedostoon, jota käsittelemme tunnilla. Kyseessä on Solage-nimisen säveltäjän teoksesta Fumeux fumes irrotettu diskanttimelodia.
fumeux_sopr.csv
Säveltäjä kuuluu ns. Ars Subtilior -kouluun 1300 luvulla. Aika hienoa musiikkia!
http://www.pacificnet.net/~garyrich/subtilior/
Tällä luennolla käyn läpi tilastotieteeseen liittyviä asioita ja käsitteitä - vauhdilla... Tarkoituksenani on, että tilastomenetelmistä ja niiden tarjoamista mahdollisuuksista jäisi jonkinlainen haju (tai - toivottavasti - paremminkin tuoksu ;-).
Tämän luentokerran jälkeen otetaan hiukan rauhallisemmin ja katsotaan, mihin suuntaan lähdetään. Keskitymme yhä enemmän R:n opiskeluun ja sovelluksiin, mutta välillä palaamme tilastojen ja tarvittaessa joukkoteorian pariin. Ja kuten tulette huomaamaan, kertaan samoja R:n komentojakin uudelleen ja uudelleen.
Mielessä on käynyt, että voisimme lähestyä kevään analyyseja esimerkiksi kahdella tavalla, markovin ketjuja hyödyntäen ja joukkoteoriaa käyttäen. Molemmat metodit ovat musiikkitieteessä käypiä eivätkä liian kuluneita, päin vastoin. Mutta muitakin tapoja varmasti keksimme ja saa ehdottaa ja niistä voisimme keskustella neljännen luentokerran jälkipuolella. Ajattelin 4. kerralla aloittaa siitä, miten R:ssä luodaan omia funktioita ja kuinka toistorakenteita (looppeja) ja ehtorakenteita R:ssä kirjoitetaan.
3. luentokalvoissa esitettyjen skriptien lopussa saadaan seuraavanlainen kuvaaja Fumeux fumes -melodiasta, josta nähdään, että se koostuu kuudesta kaarroksesta.

Laitoinpa tähän vielä linkin midi-tiedostoon musiikin kuuntelusta nauttivien iloksi!
Fumeux fumes
Erään biisin basso
EraanBiisinBasso.csv
Tuesday, January 17, 2006
2. luento 20.1.2006
2. luennon ppt-kalvot pdf-muodossa. Versio 060119c...
TKAvustMusTutk060120.pdf
Käsittelen luennolla hiukan musiikin joukkoteorian perusideoita ja -käsitteitä, kuitenkin pikaisesti. Joukkoteorian käyttäminen tietokoneavusteisessa musiikintutkimuksessa on vain yksi mahdollisuus monien joukossa, joten ei tähän tarvitse koko sydänvertaan vuodattaa. Osalla on jokin joukkoteoriaan liittyvä kurssi käytynä tai muuten kiinnostusta aiheeseen, joten joku voi löytää tältä suunnalta analyysilleen metodin.
Lisäksi puhun hiukan miditiedostoista, mutta tärkeämpää nyt niin kuin muillakin kerroilla on mielestäni tarkastella R:n käyttöä. Tulen viipymään etenkin ppt-kalvojen sivulla 25 "R-ohjelman käyttö, osa 2 (2)".
3:lla luennolla käsittelen tilastollisia ideoita, joista saattaa löytyä sellaisenaan jokin näkökulma. Tietysti esim. musiikin joukkoteoriaa voi yhdistää myös tilastollisiin menetelmiin, mikä tkamt:ssa onkin luontevaa.
Tuon mukanani kopiot aikaisemmin mainitsemistani reference card -dokumenteista, joten niitä ei tarvitse itse printata.
Ensimmäisellä tunnilla kysyttiin R:n pakettien lataamisesta internetistä omalle koneelle. Se tapahtuu siis komentokehoitteessa komennolla install.packages("paketin nimi"), esim.
install.packages("tuneR").
OSX:ssä sen voi tehdä valitsemalla asennuskomennon valikkoriviltä komennon "Package Installer".
Paketti otetaan R-sessiossa käyttöön komennolla
library(tuneR)
TKAvustMusTutk060120.pdf
Käsittelen luennolla hiukan musiikin joukkoteorian perusideoita ja -käsitteitä, kuitenkin pikaisesti. Joukkoteorian käyttäminen tietokoneavusteisessa musiikintutkimuksessa on vain yksi mahdollisuus monien joukossa, joten ei tähän tarvitse koko sydänvertaan vuodattaa. Osalla on jokin joukkoteoriaan liittyvä kurssi käytynä tai muuten kiinnostusta aiheeseen, joten joku voi löytää tältä suunnalta analyysilleen metodin.
Lisäksi puhun hiukan miditiedostoista, mutta tärkeämpää nyt niin kuin muillakin kerroilla on mielestäni tarkastella R:n käyttöä. Tulen viipymään etenkin ppt-kalvojen sivulla 25 "R-ohjelman käyttö, osa 2 (2)".
3:lla luennolla käsittelen tilastollisia ideoita, joista saattaa löytyä sellaisenaan jokin näkökulma. Tietysti esim. musiikin joukkoteoriaa voi yhdistää myös tilastollisiin menetelmiin, mikä tkamt:ssa onkin luontevaa.
Tuon mukanani kopiot aikaisemmin mainitsemistani reference card -dokumenteista, joten niitä ei tarvitse itse printata.
Ensimmäisellä tunnilla kysyttiin R:n pakettien lataamisesta internetistä omalle koneelle. Se tapahtuu siis komentokehoitteessa komennolla install.packages("paketin nimi"), esim.
install.packages("tuneR").
OSX:ssä sen voi tehdä valitsemalla asennuskomennon valikkoriviltä komennon "Package Installer".
Paketti otetaan R-sessiossa käyttöön komennolla
library(tuneR)
Thursday, January 12, 2006
Kurssin korvaavuudesta
Tiedoksi:
Syventäviin opintoihin sisältyvällä kurssilla "Tietokoneavusteinen musiikintutkimus" S1f voi korvata aineopintoihin sisältyvän kurssin "Systemaattinen musiikinteoria", T5e (6 op).
Syventäviin opintoihin sisältyvällä kurssilla "Tietokoneavusteinen musiikintutkimus" S1f voi korvata aineopintoihin sisältyvän kurssin "Systemaattinen musiikinteoria", T5e (6 op).
Wednesday, January 11, 2006
Subscribe to:
Comments (Atom)
